Hello,
I have a recent Lenovo T14s with an i7 processor and 64GB, so I assume I should expect above average performance.
The SARIMAX loop over the parameters has done 20% in 100mn.
I am running locally in VS Code.
Is that about normal or do you think I am doing something stupid?
EDIT: I stopped it after 6h and just 30% done.
Best regards,
For:
We will build a SARIMAX model for monthly data on an industrial production time series for the 1988-2017 period. As illustrated in the first section on analytical tools, the data has been log-transformed, and we are using seasonal (lag-12) differences. We estimate the model for a range of both ordinary and conventional AR and MA parameters using a rolling window of 10 years of training data, and evaluate the RMSE of the 1-step-ahead forecast.
from joblib import Parallel, delayed
from tqdm import tqdm
train_size = 120 # 10 years of training data
test_set = industrial_production_log_diff.iloc[train_size:]
def fit_and_predict(params, train_size, industrial_production_log_diff):
p1, q1, p2, q2 = params
preds = test_set.copy().to_frame('y_true').assign(y_pred=np.nan)
aic, bic = [], []
if p1 == 0 and q1 == 0:
return None
convergence_error = stationarity_error = 0
y_pred = []
for i, T in enumerate(range(train_size, len(industrial_production_log_diff))):
train_set = industrial_production_log_diff.iloc[T-train_size:T]
try:
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
model = SARIMAX(endog=train_set.values,
order=(p1, 0, q1),
seasonal_order=(p2, 0, q2, 12)).fit(disp=0)
except LinAlgError:
convergence_error += 1
continue
except ValueError:
stationarity_error += 1
continue
preds.iloc[i, 1] = model.forecast(steps=1)[0]
aic.append(model.aic)
bic.append(model.bic)
preds.dropna(inplace=True)
if preds.empty:
return None
mse = mean_squared_error(preds.y_true, preds.y_pred)
return (p1, q1, p2, q2), [np.sqrt(mse),
preds.y_true.sub(preds.y_pred).pow(2).std(),
np.mean(aic),
np.std(aic),
np.mean(bic),
np.std(bic),
convergence_error,
stationarity_error]
# Parallel processing
results = Parallel(n_jobs=-1)(delayed(fit_and_predict)(params, train_size, industrial_production_log_diff) for params in tqdm(params))
# Filter out None results
results = {k: v for k, v in results if v is not None}
This version introduces parallel processing. 100% in ~14 minutes.
The following are some of the cells and their respective outputs just to show that the refactored code will not break anything that follows.
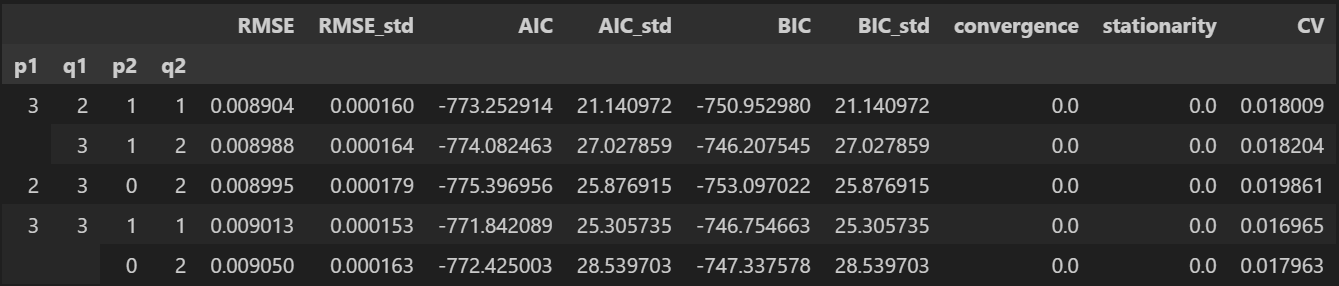
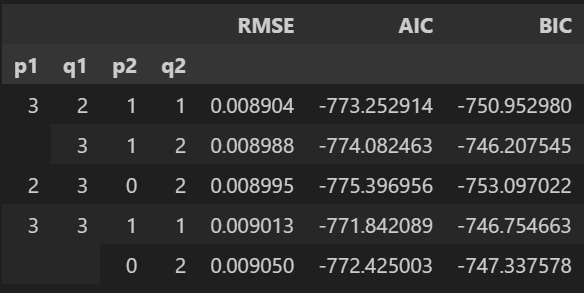
sarimax_results.nsmallest(5, columns='RMSE')
sarimax_results[['RMSE', 'AIC', 'BIC']].sort_values('RMSE').head()
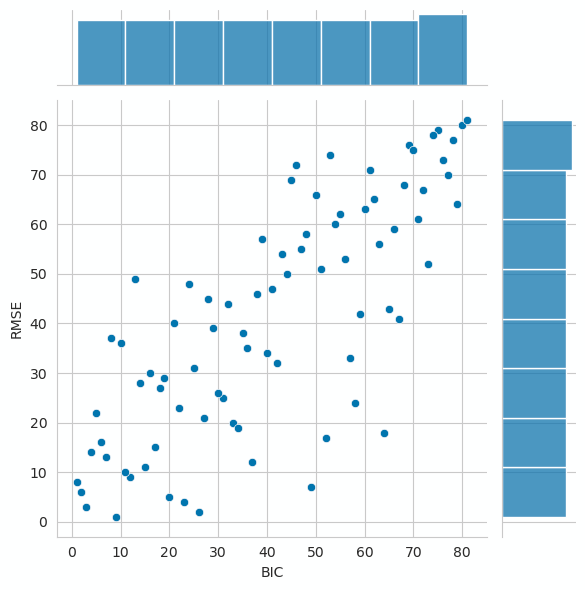
sns.jointplot(y='RMSE', x='BIC', data=sarimax_results[['RMSE', 'BIC']].rank());
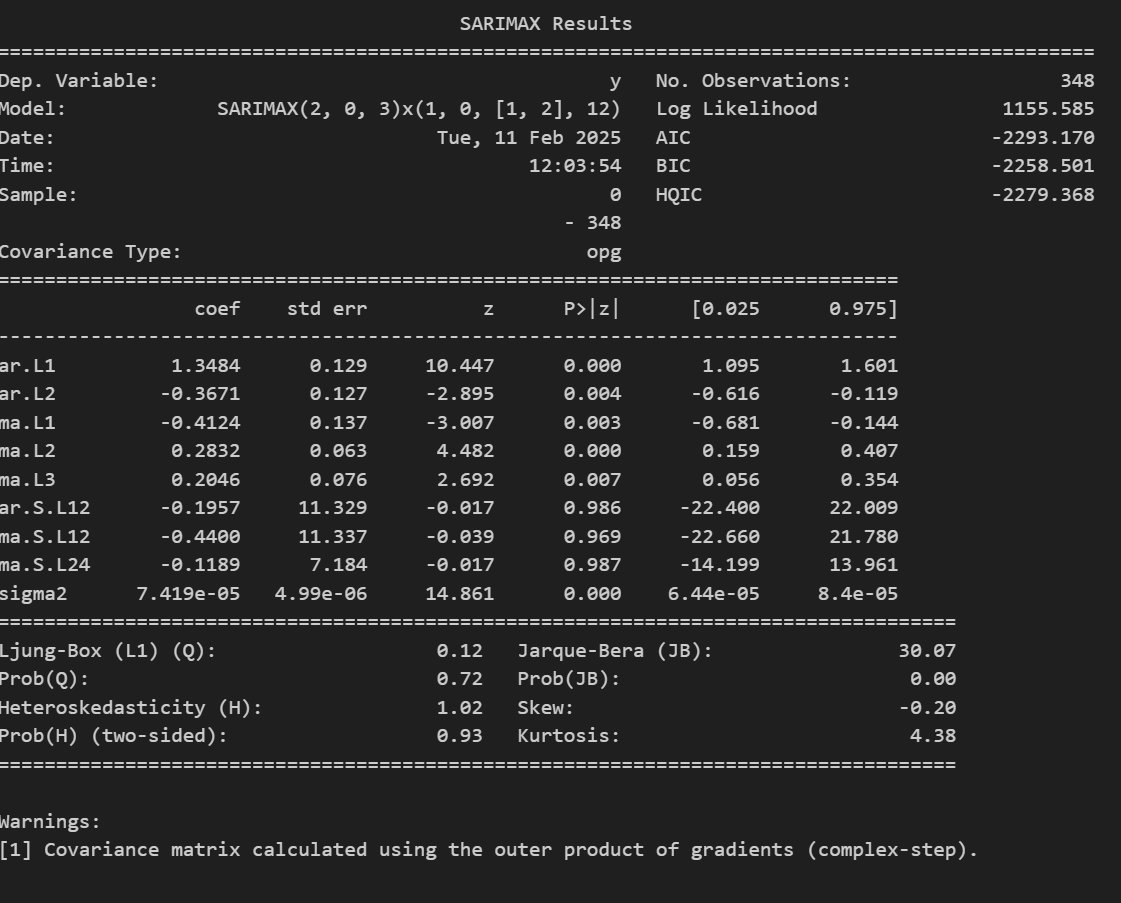
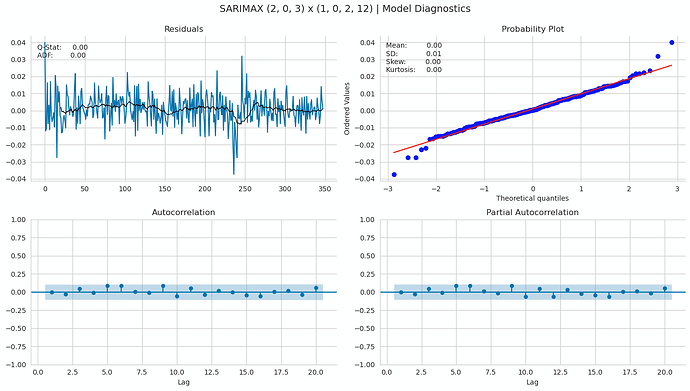
print(best_model.summary())plot_correlogram(pd.Series(best_model.resid), lags=20, title=f'SARIMAX ({p1}, 0, {q1}) x ({p2}, 0, {q2}, 12) | Model Diagnostics')
Hope this helps.
For:
We iterate over various (p, q) lag combinations and collect diagnostic statistics to compare the result.
I also replaced this:
train_size = 120
results = {}
y_true = industrial_production_log_diff.iloc[train_size:]
for p in range(5):
for q in range(5):
aic, bic = [], []
if p == 0 and q == 0:
continue
print(p, q)
convergence_error = stationarity_error = 0
y_pred = []
for T in range(train_size, len(industrial_production_log_diff)):
train_set = industrial_production_log_diff.iloc[T-train_size:T]
try:
model = tsa.ARMA(endog=train_set, order=(p, q)).fit()
except LinAlgError:
convergence_error += 1
except ValueError:
stationarity_error += 1
forecast, _, _ = model.forecast(steps=1)
y_pred.append(forecast[0])
aic.append(model.aic)
bic.append(model.bic)
result = (pd.DataFrame({'y_true': y_true, 'y_pred': y_pred})
.replace(np.inf, np.nan)
.dropna())
rmse = np.sqrt(mean_squared_error(
y_true=result.y_true, y_pred=result.y_pred))
results[(p, q)] = [rmse,
np.mean(aic),
np.mean(bic),
convergence_error,
stationarity_error]
with:
from joblib import Parallel, delayed
train_size = 120
y_true = industrial_production_log_diff.iloc[train_size:]
def fit_and_evaluate(p, q, train_size, industrial_production_log_diff, y_true):
aic, bic = [], []
if p == 0 and q == 0:
return (p, q), None
convergence_error = stationarity_error = 0
y_pred = []
for T in range(train_size, len(industrial_production_log_diff)):
train_set = industrial_production_log_diff.iloc[T-train_size:T]
try:
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
model = ARIMA(endog=train_set, order=(p, 0, q)).fit()
except LinAlgError:
convergence_error += 1
continue
except ValueError:
stationarity_error += 1
continue
forecast = model.forecast(steps=1)
y_pred.append(forecast.iloc[0])
aic.append(model.aic)
bic.append(model.bic)
result = (pd.DataFrame({'y_true': y_true.iloc[:len(y_pred)].values, 'y_pred': y_pred})
.replace(np.inf, np.nan)
.dropna())
if result.empty:
return (p, q), None
rmse = np.sqrt(mean_squared_error(y_true=result.y_true, y_pred=result.y_pred))
return (p, q), [rmse, np.mean(aic), np.mean(bic), convergence_error, stationarity_error]
# Parallel processing
params = [(p, q) for p in range(5) for q in range(5)]
results = Parallel(n_jobs=-1)(delayed(fit_and_evaluate)(p, q, train_size, industrial_production_log_diff, y_true) for p, q in tqdm(params))
# Filter out None results
results = {k: v for k, v in results if v is not None}
print(results)
Which will output the dictionary but you can omit the print(results) line if you so opt to. This runs in ~1.5 minutes.